Ментальная арифметика: что это такое и как этому научиться?

Вы же видели видеоролики, где дети активно размахивают руками, будто бы играют на невидимом музыкальном инструменте?
Да, согласны, выглядит слегка странновато и непривычно. Примерно как скандинавская ходьба лет 15 назад. Но так же, как и у ходоков с палками по городу, у детей, размахивающих руками, есть свои причины так делать. Таким образом они решают сложные математические задачи.
В этом и заключается суть ментальной арифметики — методики, позволяющей выполнять вычисления в уме с поразительной скоростью и точностью. А движения рук — это следы работы с азиатским абаком (соробаном), который и лежит в основе обучения.

Если в предыдущем абзаце вы увидели два незнакомых вам слова — не спешите их гуглить, ниже мы расскажем что такое соробан и что такое абак.
А пока уделим внимание самой методике, которая пришла к нам из стран Восточной Азии, таких как Япония и Китай. И которая сегодня набирает популярность по всему миру, включая Россию.
Ментальная арифметика простыми словами
Это техника, которая не просто учит детей складывать и вычитать числа в уме быстрее калькулятора, но и развивает их когнитивные способности: концентрацию, память, воображение и даже творческое мышление. В основе ментальной арифметики лежит использование соробана — традиционного счёта, который превращает абстрактные цифры в зримые образы.
Но как это работает? И почему школьники, освоившие эту методику, порой решают примеры вроде 456 + 789 или даже 2345 × 67 быстрее, чем взрослые с калькулятором? Давайте разберёмся.
Истоки ментальной арифметики

Ментальная арифметика, какой мы её знаем сегодня, тесно связана с традициями Восточной Азии, но её корни уходят в глубокую древность, к первым счётным инструментам человечества.
История абаков начинается ещё в III тысячелетии до н.э. в Древнем Вавилоне, где для вычислений использовались простейшие устройства — доски с бороздками, заполненными песком, или камешки, которые передвигали для подсчёта. Эти примитивные абаки стали прародителями всех последующих счётных инструментов.
Однако ментальная арифметика как методика, основанная на визуализации и быстрых вычислениях в уме, оформилась значительно позже благодаря эволюции азиатских абаков — китайского суаньпаня и японского соробана.
Древний Вавилон: начало пути
Самые ранние свидетельства использования абаков относятся к Месопотамии, примерно к 2700–2300 гг. до н.э. Вавилоняне применяли их для сложения и вычитания в своей шестидесятеричной системе счисления, которая использовалась в торговле и астрономии.
Это были не счёты в современном понимании, а скорее приспособления для работы с числами, где камни или метки обозначали единицы, десятки и более крупные разряды. Хотя такие инструменты уже демонстрировали стремление человека упростить вычисления, они оставались далёкими от систематизированной методики, которая позже появится в Азии.
Позже абаки распространились в Древнем Египте (около 2000 г. до н.э.) и Древней Греции (около 500 г. до н.э.), где их совершенствовали для нужд торговли и науки. Однако эти ранние версии не имели той структуры и универсальности, которые позже сделали азиатские счёты основой ментальной арифметики.
Китайский суаньпань
Настоящий прорыв в развитии абаков произошёл в Китае с появлением суаньпаня (от кит. 算盘, «счётная доска»). Хотя точная дата его изобретения неизвестна, первые упоминания относятся к эпохе династии Хань (202 г. до н.э. – 220 г. н.э.), а широкое распространение он получил в XII–XIII веках во времена династии Юань.
Суаньпань состоял из деревянной рамки с вертикальными стержнями, на которых находились костяшки: две в верхней части (каждая по 5) и пять в нижней (каждая по 1). Эта структура позволяла быстро работать с десятичной системой, что идеально подходило для сложных вычислений.

Китайские торговцы и учёные использовали суаньпань для подсчёта налогов, измерения земель и даже астрономических расчётов. Инструмент был настолько эффективен, что оставался в ходу до XX века.
Именно суаньпань заложил основу для визуализации чисел — ключевого принципа ментальной арифметики, когда абстрактные цифры превращаются в осязаемые образы.
Японский соробан
В XIV веке суаньпань попал в Японию через торговые связи с Китаем и был усовершенствован в соробан (от яп. 算盤, «счётная доска»).
Японцы упростили конструкцию: одна костяшка в верхней части (равная 5) и четыре в нижней (каждая по 1). Это сделало соробан более компактным и быстрым в использовании. К периоду Эдо (1603–1868 гг.) он стал неотъемлемой частью японской культуры и образования.

В XIX веке в японских школах начали обучать детей работе с соробаном, а соревнования по счёту выявили удивительную способность некоторых учеников: они могли выполнять вычисления, не касаясь инструмента, представляя его в уме.
Это стало первым шагом к ментальной арифметике как методике. Например, мастера соробана могли складывать десятки многозначных чисел за секунды, что поражало даже европейских математиков того времени.
Современность
После Второй мировой войны соробан стал частью японской школьной программы, а в 1950-х годах методика начала распространяться за пределы Азии.
Исследователи, такие как японский нейрофизиолог доктор Тосихико Койке, в своих работах (например, в работе Университета Осаки, 2001 г.) показали, что работа с соробаном активирует оба полушария мозга, улучшая память и концентрацию. Это привлекло внимание педагогов Южной Кореи, Индии, а затем Европы и России.
Что такое соробан и как он устроен?
Соробан представляет собой прямоугольную рамку с вертикальными стержнями, на которых расположены косточки (бусины). Обычно в соробане 13–23 стержня, каждый из которых соответствует определённому разряду числа (единицы, десятки, сотни и т.д.). На каждом стержне находится 5 бусин, разделённых горизонтальной перекладиной:
1 бусина над перекладиной имеет значение 5;
4 бусины под перекладиной имеют значение 1 каждая.
Пример: чтобы показать число 7 на одном стержне, нужно сдвинуть к перекладине одну бусину "5" и две бусины "1". Таким образом, соробан позволяет визуализировать числа и операции с ними.
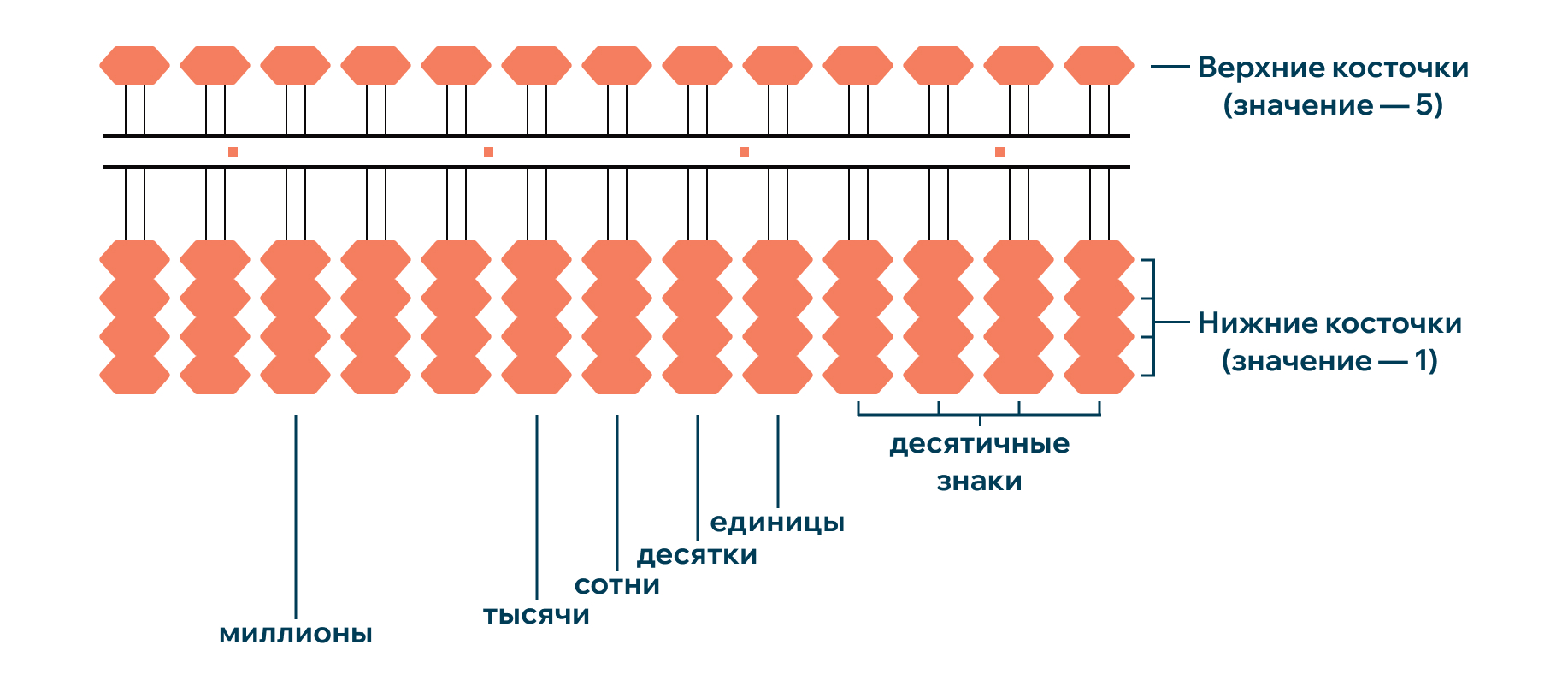
Суаньпань, китайский аналог, немного отличается: на каждом стержне 7 бусин (2 над перекладиной со значением 5 и 5 под перекладиной со значением 1), но принцип действия схож.
Как работает ментальная арифметика?
Ментальная арифметика начинается с физического использования соробана. Ученики учатся выполнять базовые операции — сложение, вычитание, умножение и деление — двигая бусины пальцами.
Техника требует точных движений и понимания позиционной системы счисления. Например:
Чтобы сложить 23 и 45, ученик сначала выставляет 23 на соробане (2 десятка и 3 единицы), затем добавляет 45 (4 десятка и 5 единиц), сдвигая бусины и перенося десятки при необходимости.
При вычитании используется обратный процесс, а умножение и деление разбиваются на последовательности сложений и вычитаний.
После освоения физического инструмента начинается ключевой этап — переход к ментальным вычислениям. Ученики визуализируют соробан в уме и "двигают" воображаемые бусины, повторяя те же действия, что и с реальным абаком.
Этот процесс требует развитой зрительной памяти и концентрации. Со временем скорость вычислений возрастает, и человек может решать задачи вроде 345 + 672 или 89 × 43 за секунды без калькулятора.
Научное подтверждение эффективности

Исследования показывают, что ментальная арифметика с абаками положительно влияет на когнитивные способности. В 2016 году японские ученые из Университета Осаки опубликовали в журнале Developmental Neuropsychology данные, согласно которым дети, обучавшиеся с соробаном, демонстрировали улучшение рабочей памяти и скорости обработки информации по сравнению с контрольной группой. МРТ-сканирование показало повышенную активность в правом полушарии мозга, ответственном за пространственное мышление, у тех, кто регулярно практиковал ментальные вычисления.
Кроме того, в 2018 году исследование в Южной Корее (опубликовано в Journal of Cognitive Enhancement) подтвердило, что дети 7–12 лет, обучавшиеся ментальной арифметике, лучше справлялись с задачами на концентрацию и решением математических заданий, чем их сверстники.
Что даёт ментальная арифметика?
Развитие мозга: Работа с соробаном активирует оба полушария мозга — левое (логика) и правое (визуализация), улучшая нейронные связи.
Улучшение памяти: Визуализация тренирует кратковременную и долговременную память.
Скорость вычислений: Даже сложные задачи решаются быстрее, чем с калькулятором.
Концентрация: Регулярные занятия повышают способность фокусироваться на задаче.
Уверенность: Дети, освоившие методику, лучше справляются с математикой в школе и чувствуют себя успешнее.
Интересный факт: В Японии ментальная арифметика с соробаном остаётся популярной — около 2 миллионов детей ежегодно обучаются по этой системе (данные Soroban Foundation, 2020). В Китае методика интегрирована в программы подготовки к экзаменам, где требуется быстрое решение задач. В России ментальная арифметика начала набирать популярность в 2010-х годах, и сегодня в крупных городах работают центры вроде "Амакидс" или "Соробан", обучающие детей от 5 до 14 лет.
Пример задачи для уровня "начинающий": сложить 47 и 58. На соробане это делается так:
- Выставляем 47: 4 десятка и 7 единиц (верхняя косточка 5 + две нижние 2).
- Добавляем 58: Прибавляем 5 десятков (становится 9 десятков) и 8 единиц.
- Перенос в единицах: 7 единиц + 8 единиц = 15. 10 единиц превращаем в 1 десяток (добавляем его к десяткам). Остается 5 единиц.
- Перенос в десятках: Теперь у нас 9 десятков + 1 десяток (от переноса) = 10 десятков. 10 десятков превращаем в 1 сотню (выставляем в разряд сотен). В десятках остаётся 0.
- Итог: Сотни: 1, Десятки: 0, Единицы: 5. Ответ: 105.
С опытом такие операции выполняются в уме за 1–2 секунды.
Когда лучше начинать обучение ментальной арифметике?

Оптимальный возраст для начала обучения ментальной арифметике с использованием соробана — от 5 до 12 лет, когда мозг ребёнка активно развивается, а нейронные связи формируются быстрее всего. В это время дети легко осваивают базовые операции и переходят к ментальным вычислениям, улучшая память и концентрацию. Исследование 2016 года из Университета Осаки (опубликовано в Developmental Neuropsychology) показало, что дети 6–12 лет, обучавшиеся счёту с соробаном, улучшали рабочую память на 20–30% быстрее, чем взрослые.
Для малышей 3–4 лет обучение возможно в игровой форме, но ограничивается простыми действиями из-за короткого периода концентрации внимания и слабого абстрактного мышления. Исследование 2019 года из Южной Кореи (Journal of Early Childhood Education) показало, что дети 4 лет улучшают координацию и распознавание чисел на 15% после 3 месяцев работы с соробаном, но ментальные навыки остаются недоступными.
Подростки 13–18 лет могут учиться быстрее благодаря школьным навыкам, но пластичность мозга уже снижается. Взрослые (18+ лет) тоже способны освоить методику, особенно для работы или хобби, хотя ментальные вычисления даются сложнее и требуют больше времени — до 1–2 лет против 6–12 месяцев у детей.
| Возраст | Преимущества | Ограничения | Рекомендация |
| 3–4 года | Развитие моторики, знакомство с числами | Недостаток внимания, нет ментальных навыков | Игровая форма, не более 15 минут |
| 5–12 лет | Пик пластичности мозга, быстрый прогресс | — | Лучшее время для начала |
| 13–18 лет | Быстрое понимание, мотивация для учёбы | Снижение пластичности мозга, занятость | Подходит при дисциплине |
| 18+ лет | Практическая польза, осознанность | Медленный переход к ментальным навыкам | Реально при регулярности |
Начинать лучше всего в 5–12 лет, но успех возможен в любом возрасте при регулярных занятиях по 15–30 минут в день.
Как научиться ментальной арифметике? Объясняем пошагово
Приводим конкретный, пошаговый план обучения, основанный на проверенных методиках, используемых в образовательных центрах, таких как японская система Soroban Foundation, китайская CMA (Chinese Mental Arithmetic). Все шаги подкреплены реальными примерами и рекомендациями.
Шаг 1: Приобретите соробан и разберитесь с его устройством

от 500 до 1500 рублей, в зависимости от качества и размера. Для новичков подойдёт модель с 13–17 стержнями — этого достаточно, чтобы работать с числами до миллионов, не перегружая себя лишними разрядами.
При выборе обратите внимание на то, чтобы на каждом стержне было 5 бусин: одна над горизонтальной перекладиной (со значением 5) и четыре под ней (каждая со значением 1). Качественный соробан должен иметь прочный каркас и легко скользящие бусины, чтобы движения пальцев были плавными.
Как только соробан у вас в руках, начните с изучения его структуры. Представьте, что это не просто инструмент, а способ визуализировать числа. Каждый стержень соответствует определённому разряду: самый правый — единицы, следующий слева — десятки, затем сотни и так далее.
Чтобы освоиться, попробуйте выставить несколько простых чисел. Например:
Для числа 3 сдвиньте три бусины "1" на первом стержне справа к перекладине — это легко сделать большим и указательным пальцами.
Для числа 7 используйте одну бусину "5" (над перекладиной) и две бусины "1" (под ней) — это уже требует координации, но быстро становится привычным.
Число 45 потребует работы с двумя стержнями: на стержне десятков сдвиньте четыре бусины "1", а на стержне единиц — одну бусину "5".
Проведите с этим 1–2 часа, пробуя числа вроде 19, 62 или 104, чтобы почувствовать логику.
Этот этап критически важен, потому что соробан — не просто калькулятор, а система, которая учит видеть числа как физические объекты. В японских школах, таких как Soroban Foundation, первый урок полностью посвящён этому: ученики трогают бусины, называют числа и привыкают к их расположению.
Учебник "Soroban: The Japanese Abacus" Такаси Кодзимы советует не торопиться и потратить хотя бы день на то, чтобы уверенно выставлять числа до 100. Если вы чувствуете, что пальцы слушаются, а числа "оживают" на соробане, можно двигаться дальше.
Шаг 2: Освойте базовые операции на соробане

Теперь, когда соробан стал знакомым, пора научиться считать на нём. Начнём с простого сложения и вычитания — это фундамент, на котором строятся все дальнейшие навыки.
Возьмём пример сложения: 23 + 45. Сначала выставьте 23 на соробане: на стержне десятков сдвиньте две бусины "1", а на стержне единиц — три бусины "1". Затем добавьте 45. К двум десяткам прибавьте четыре — получится шесть, что легко показать шестью бусинами "1" или одной "5" и одной "1". К трём единицам прибавьте пять — получится восемь (одна бусина "5" и три "1"). Итог — 68. Это кажется простым, но требует точности движений. Потренируйтесь на задачах вроде 15 + 27 или 34 + 19, решая по 10 примеров за 15 минут, чтобы руки запомнили процесс.
Вычитание работает по обратному принципу. Возьмём 58 – 23. Выставьте 58: на стержне десятков — одна бусина "5", на стержне единиц — одна "5" и три "1". Уберите 23: от десятков отнимите две бусины (остаётся три), от единиц — три (восемь минус три равно пять, просто оставьте одну бусину "5"). Итог — 35. Попробуйте задачи вроде 47 – 19 или 82 – 36, повторяя по 10 примеров ежедневно.
На этом этапе важно не спешить: 1–2 недели по 20–30 минут в день закрепят навык. В системе CMA первые 10–15 занятий посвящены только таким операциям с числами до 100, чтобы ученики довели движения до автоматизма. Учебник "Abacus Mind Math Level 1" предлагает таблицы сложения и вычитания — их можно найти онлайн или распечатать для практики.
Шаг 3: Научитесь работать с переносом и заимствованием

Когда базовые операции освоены, пора усложнить задачу переносом и заимствованием — это ключ к работе с многозначными числами.
Для вычитания с заимствованием возьмём 62 – 38. Выставьте 62: шесть бусин "1" на десятках, две "1" на единицах. Уберите 38: от двух единиц не отнять восемь, поэтому заимствуйте один десяток. Шесть десятков минус один — пять, а две единицы плюс десять дают 12. Теперь 12 минус 8 равно 4, а из пяти десятков уберите три — остаётся два. Итог — 24. Это чуть сложнее, но после 20 задач вроде 85 – 47 или 73 – 29 процесс станет привычным.
В японских соревнованиях по ментальной арифметике такие задачи — обязательная часть базового уровня, и ученики тренируются до тех пор, пока не перестают ошибаться.
Шаг 4: Освойте умножение и деление

Следующий этап — умножение и деление, которые требуют разбивки на шаги.
Для умножения рассмотрим 13 × 4. Разложите 13 на 10 и 3: 10 умножить на 4 равно 40, 3 умножить на 4 равно 12, затем сложите 40 и 12, получив 52. На соробане это можно сделать, добавляя 13 четыре раза: выставьте 13 и повторяйте сложение с учётом переносов. Начните с простых примеров вроде 5 × 6 или 7 × 8, постепенно переходя к двузначным числам, таким как 12 × 15.
Деление работает наоборот. Для 84 ÷ 4 выставьте 84 и делите по разрядам: восемь десятков делим на 4 — два десятка, четыре единицы делим на 4 — одна единица. Итог — 21. Практикуйтесь на задачах вроде 36 ÷ 3 или 95 ÷ 5, решая по 10 примеров в день.
На это уйдёт 2–4 недели по 30 минут ежедневно, как описано в книге Такаси Кодзимы "The Japanese Abacus: Its Use and Theory".
Шаг 5: Переходите к ментальным вычислениям

Когда физический соробан освоен, начинается самое интересное — вычисления в уме. Закройте глаза и представьте соробан: стержни, бусины, перекладину.
Возьмём 34 + 27: мысленно выставьте три десятка и четыре единицы, добавьте два десятка и семь единиц. Четыре плюс семь равно 11 — оставьте одну единицу и перенесите десяток, получив пять десятков и одну единицу, итог — 61. Для тренировки используйте карточки Anzan Flash Cards (доступны онлайн) или приложение "Soroban Anzan". Сначала решайте 10–20 задач в день, тратя 5–10 секунд на каждую, затем ускоряйтесь до 1–2 секунд.
Этот этап занимает 1–2 месяца по 15–30 минут в день. В CMA программе переход к ментальным вычислениям начинается после 3–6 месяцев, и ученики уже показывают результаты на тестах.
Шаг 6: Регулярная практика и усложнение

Финальный шаг — закрепление и развитие навыков.
Переходите к многозначным числам: сложите 345 + 672 или умножьте 89 × 43 в уме. Тренируйтесь 20–30 минут в день, включая 5 минут на скоростные задачи — например, сложение десяти пятизначных чисел.
Японские мастера, такие как Юки Кимура, чемпион мира 2016 года, решают до 100 задач за 1–2 часа ежедневно, показывая, что регулярность — ключ к мастерству.
Кстати, в России проходит "Соробан Олимпиада". Можете участвовать в ней.

Заключение
Как мы уже сказали, ментальная арифметика с соробаном высоко ценится многими специалистами за её влияние на когнитивные способности. Давайте пробежимся по экспертам ещё раз. Только теперь и скептиков упомянем.
Сторонники метода:
- Японские учёные из Университета Осаки (исследование 2016 года, Developmental Neuropsychology) подтверждают, что дети, обучавшиеся счёту на соробане, улучшают рабочую память и скорость обработки информации, а МРТ показывает повышенную активность в правом полушарии, связанном с пространственным мышлением.
- В Южной Корее исследование 2018 года (Journal of Cognitive Enhancement) показало, что ученики 7–12 лет, работавшие с соробаном, лучше справляются с задачами на концентрацию и математическими вычислениями.
- Педагоги из Soroban Foundation подчёркивают, что метод развивает дисциплину и уверенность, особенно у детей 5–12 лет, что делает его популярным в Азии и за её пределами.
Теперь про критиков:
- Некоторые нейропсихологи, например, Джон Майкл из Университета Уорвика (статья 2019 года в Educational Psychology Review), считают, что преимущества ментальной арифметики преувеличены. Они указывают на то, что улучшение памяти и концентрации может быть связано не столько с соробаном, сколько с общей практикой счёта, и сравнимые результаты дают другие методы, вроде шахмат или музыкальных занятий.
- Есть мнение, что навык быстрых вычислений теряет практическую ценность в эпоху калькуляторов и смартфонов — критики, такие как педагог Марк Шварц в книге "Math Education in the Digital Age" (2021), называют это "устаревшим трюком", полезным разве что для соревнований.
- Кроме того, исследования (например, из журнала Cognitive Science, 2020) показывают, что эффект сильно зависит от регулярности: без ежедневных тренировок навыки угасают, а для многих детей и взрослых это становится нагрузкой, снижая мотивацию.
Подытожим:

Объективно, ментальная арифметика с соробаном для детей и взрослых — это мощный инструмент развития мозга, особенно для подрастающего поколения, но не универсальное решение. Её успех доказан в конкретных областях — память, скорость счёта, концентрация, — но он требует времени и усилий, а польза может быть ограничена, если цель не связана с математикой или когнитивным ростом.
Если вы готовы к дисциплине, метод оправдает себя; если нет, то это может оказаться просто интересным, но необязательным опытом. В общем, попробуйте сами и решите, стоит ли оно того.





































